汉振分享 | 包围盒在点云ROI和碰撞检测中的应用

01 概述
包围盒是一种求解离散点集最优包围空间的算法，基本思想是用体积稍大且特性简单的几何体（称为包围盒）来近似地代替复杂的几何对象。常见的包围盒算法有AABB包围盒、包围球、有向包围盒OBB以及固定方向凸包FDH。

图1. 3D包围盒

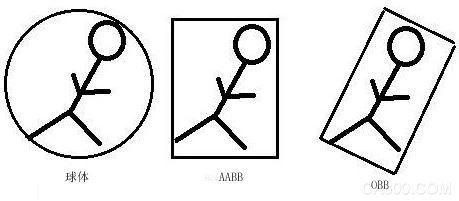
图2.  2D包围盒
OBB这种方法是根据物体本身的几何形状来决定盒子的大小和方向，盒子无需和坐标轴垂直。这样就可以选择最合适、最紧凑的包容盒子。OBB盒子的生成比较复杂。一般是考虑物体所有的顶点在空间的分布，通过一定的算法找到最好的方向(OBB盒子的几个轴)。
包围球是用球体包围整个几何体, 无论是几何体还是相交测试都很简单，但是它的紧密性太差。因为除了在3 个坐标轴上分布得比较均匀的几何体外, 几乎都会留下较大的空隙，需要花费大量的预处理时间，以构造一个好的层次结构逼近对象。当物体变形之后，包围球不需要重新计算。因此，它是使用得比较少的一种包围盒。当对象发生旋转运动时，包围球不需作任何更新，这是包围球的较优秀特性；当几何对象进行频繁的旋转运动时，采用包围球可能得到较好结果。

AABB就是3D一个简单的六面体，每一边都平行于一个坐标平面，矩形边界框不一定都是立方体，它的长、宽、高可以彼此不同。

02 包围盒在3D点云分割中的应用

1. 三维点云分割是将同属性的点云物体分割出来，以便于单独对该点云物体处理，以下是借助PCL点云库寻找点云的最小包围盒的实现原理。
2. 最小包围盒的计算过程大致如下：
3. 利用PCA主元分析法获得点云的三个主方向，获取质心，计算协方差，获得协方差矩阵，求取协方差矩阵的特征值和特长向量，特征向量即为主方向。
4. 利用获得的主方向和质心，将输入点云转换至原点，且主方向与坐标系方向重合，建立变换到原点的点云的包围盒。
5. 给输入点云设置主方向和包围盒，通过输入点云到原点点云变换的逆变换实现。
6. 输入点云转换至远点后，求得变换后点云的最大最小x,y,z轴的坐标,如 (max.x,max.y,max.z),(max.x,min.y,max.z),(max.x,max.y,min.z),(min.x,max.y,max.z),(min.x,max.y,min.z),(min.x,min.y,max.z),(min.x,min.y,max.z),(min.x,min.y,min.z)，即为变换后点云的包围盒，也是原始输入点云包围盒顶点坐标经过变化后的坐标。将上述求得的８个包围盒坐标逆变换回输入点云的坐标系，即得到原始输入点云的包围盒顶点坐标。

实现效果如下图：

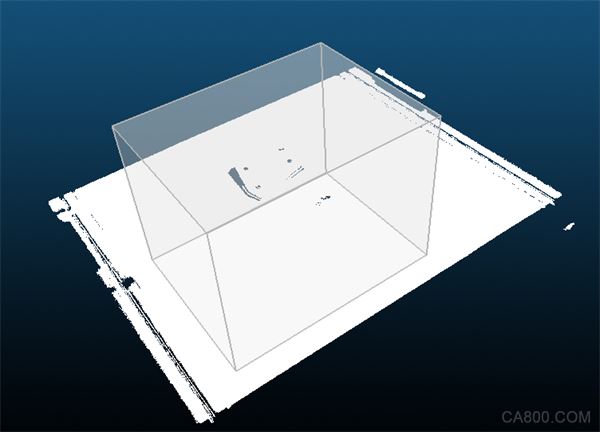
图3. 点云分割前

图4. 点云分割后

03 包围盒在碰撞检测中的应用
在碰撞检测中，为减少计算消耗，在进行相交测试前，可以先进行粗略的包围体（BV）测试。对于某些应用程序，包围体测试足以提供碰撞检测依据。一般情况下，包围体计算须采用预处理而非实时计算。当包围体所包含的对象移动时，一些包围体需要实现空间重对齐。
包围体的期望特征：

1. 低消耗的相交测试
2. 实现紧密拟合
3. 计算耗费较少
4. 易于旋转和变换
5. 内存占用较少

包围体主要包含球体、轴对齐包围盒（AABB）、有向包围盒（OBB）、8-DOP以及凸壳，以下仅对轴对齐包围盒（AABB）在碰撞检测的实现原理。
轴对齐包围盒（AABB）是应用最广泛的包围体之一。其最大特点是能实现快速的相交测试，即仅执行相应的坐标值之间的比较。
 轴对齐包围盒（AABB）有3种常规表达方式：
  1.采用各坐标轴上的最小值和最大值
//region R = (x,y,z) | min.x <= x <= max.x, min.y <= y <= max.y, min.z <= z <= max.z
struct AABB {
    Point min;
    Point max;
};
    AABB间的相交测试
bool Collision(AABB a, AABB b) {
    //Exit with no intersection if separated along an axis
    if(a.max[0] < b.min[0] || a.min[0] > b.max[0]) return false;
    if(a.max[1] < b.min[1] || a.min[1] > b.max[1]) return false;
    if(a.max[2] < b.min[2] || a.min[2] > b.max[2]) return false;
    //Overlapping on all axes means AABs are intersecting
    return true;
} 
  2.采用一个最小顶点值和直径范围dx,dy,dz
//region R = (x,y,z) | min.x <= x <= min.x + dx, min.y <= y <= min.y + dy, min.z <= z <= min.z + z
struct AABB {
    Point min;
    float d[3];
};
    AABB间的相交测试
bool Collision(AABB a, AABB b) {
    float t;
    if((t = a.min[0] - b.min[0]) > b.d[0] || -t > a.d[0]) return false;
    if((t = a.min[1] - b.min[1]) > b.d[1] || -t > a.d[0]) return false;
    if((t = a.min[2] - b.min[2]) > b.d[2] || -t > a.d[0]) return false;
    return true;
}
  3.给定AABB的中心点C，以及各轴向半径rx,ry,rz
//region R = (x, y, z) | |c.x - x| <= rx, |c.y - y| <= ry, |c.z - z| <= rz
struct AABB {
    Point c;
    float r[3];
};
    AABB间的相交测试
bool Collision(AABB a, AABB b) {
    if(Abs(a.c[0] - b.c[0]) > (a.r[0] + b.r[0])) return false;
    if(Abs(a.c[1] - b.c[1]) > (a.r[1] + b.r[1])) return false;
    if(Abs(a.c[2] - b.c[2]) > (a.r[2] + b.r[2])) return false;
    return true;
}
对于需要执行大量相交测试的碰撞检测系统，可根据状态的相似性对测试进行排序。例如：如果相应操作基本出现在xz平面，则y坐标测试应最后执行，从而使状态的变化降低到最小程度。
 若物体只是以平移方式运动，与“最大-最小值”方式相比，另外两种更加方便——只需要更新6个参数中的3个（即Point中的x,y,z）。
对于AABB的计算与更新，在此仅列出以下4种基本方法：

1. 使用固定尺寸且较为松散的AABB包围物体对象
2. 基于原点确定动态且紧凑的重构方式
3. 利用爬山法确定动态且紧凑的重构方式
4. 基于旋转后的AABB，确定近似且动态的重构方式