
基于数字条纹投影(DFP)的三维光学形状测量技术因其条纹生成灵活、设备易于搭建且价格相对便宜等特点在各个非接触实时测量领域引起了广泛关注。对于基于DFP的三维形状测量技术,相位展开至关重要,因为无论是使用相移算法还是傅里叶变换方法分析条纹图,都只能获得从-𝜋到+𝜋的包裹相位。为了展开相位,必须通过加上或减去2𝜋的多个整数周期来识别和移除2𝜋的不连续性。在一个点(x,y)上加上2𝜋的数目通常被称为条纹级数k(x,y)。基本上,相位展开就是确定每个点的k(x,y),以便可以正确地展开被包裹的相位。尽管已经开发了许多相位展开算法,但是总的来说传统的相位展开方法可以分为两类:空间相位展开和时间相位展开。

一般正弦条纹图可以用如下公式表达:
可以采用傅里叶变换或者相移方法恢复相位值。这些算法本质上使用一个反正切函数计算逐像素的相位值,所以相位值范围在-𝜋到+𝜋或0到2𝜋。此阶段获得的相位称为包裹相位。在恢复三维坐标之前需要进行相位展开,将整数倍的2 𝜋添加到包裹相位上。
这种方法通过局部或全局优化,参照同一相位图上其他点的相位值来展开相位。由Ghiglia和Pritt[2]编辑的这本书总结了许多空间相位展开方法。目前最流行、最稳健、最有效的空间相位展开方法是使用质量图来引导展开路径。质量引导相位展开的基本思想是在质量较低的相位点之前展开质量较高的相位点,这样误差就不会传播到其他点。如下图示意:
常见的几种质量图包括相关质量图、伪相关质量图、相位导数偏差质量图、最大相位梯度质量图,相关介绍如下[3]:

相关质量图是干涉合成孔径雷达包裹相位图所特有的一种质量图,它是由干涉合成孔径雷达数据的相关系数来定义的。设um,n , vm,n 是两幅合成孔径雷达数据在(m, n)处的复信号,则(m, n)处的相关质量定义为:

相关质量图是对干涉合成孔径雷达数据质量的一种较优估计,但因其只适用于合成孔径雷达图像数据,不适用于表征光学干涉测量术和医学磁共振成像获得的包裹相位图质量。

伪相关质量图是在合成孔径雷达图像数据中有关几何数据未知的情况下,对相关质量图的一种模拟和简化。包裹相位图中(m, n)处的伪相关质量定义为:

尽管伪相关质量图是对相关质量图的一种模拟,它却可以从包裹相位数据直接得到,因此可以表征由各种方法获得的包裹相位图的质量,而不仅仅局限于干涉合成孔径雷达图像的相位展开。在具有较大梯度的局域中,伪相关质量图对干涉合成孔径雷达数据质量的估计不如相关质量图好。

相位导数偏差质量图用于表示包裹相位数据导数的统计变化特征,包裹相位图中(m, n) 处的相位导数偏差定义为:

相位导数偏差质量图可以从包裹相位数据直接得到,目前它被认为是对包裹相位数据质量最可靠的估计。

最大相位梯度是对每个像素的邻域窗口内最大相位梯度的计量。用最大相位梯度作为包裹相位数据质量的评定标准,是因为在噪声较大的区域,相位梯度一般都比较大。因此,用这种质量图可以较好地识别噪声区域。包裹相位图中(m, n)处的最大相位梯度定义为:
与伪相关质量图和相位导数偏差质量图相同,最大相位梯度质量图也可以从包裹相位数据直接获得。但是在具有较大梯度的局域中,最大相位梯度质量图常会低估包裹相位质量值。

在基于光栅投影的三维面形测量中,条纹的调制度可以用于衡量包裹相位数据质量的好坏。比如在阴影、背景或轮廓不连续区域,包裹相位数据是不可靠的,这些区域可以由其对应的低调制度而被识别出来。因此,调制度可以作为一种质量图来评价包裹相位数据的可靠程度。对于 N 步相移相位测量轮廓术中,包裹相位图中(m, n)处的调制度定义为:

对于包裹相位图,调制度质量图也是一种较可靠的估计,但是这种质量图不能直接从包裹相位数据获得,必须从获得的原始条纹图中得到。

无论空间相位以怎样的算法展开,它基本上都受到曲面平滑假设的限制:对象曲面必须平滑到至少一条展开路径,以便对象曲面几何体在两个连续点之间不会引入超过𝜋的相位变化。
时间相位展开基于在不同时间获得的额外图片信息来确定每个点的条纹级数k(x,y)。在该方法中,不需要知道相位图上其他点的相位值,就可以根据额外获得的信息来确定条纹的级数,因此时间相位展开方法通常产生绝对条纹级数,并且展开的相位是绝对的。由于DFP系统可以灵活地产生不同形式的结构图,使绝对相位展开有了更多的方法。常见的方法有二进制编码、多频相移、散斑等方式。

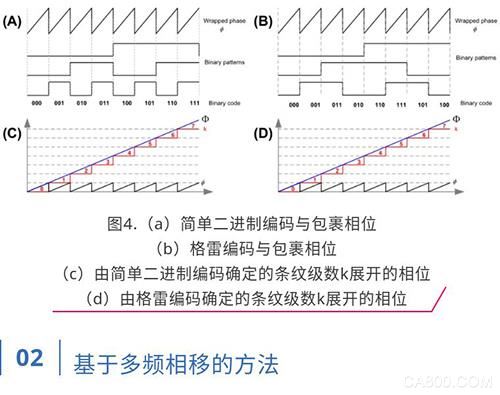
最直接的方法是直接将条纹级数k(x,y)编码成一系列二值图案。理论上,可以利用三维形状测量系统中所有二进制编码方法。这些编码方法可以是简单编码[4]、条带边界编码[5]、格雷编码[6]以及任何改进的编码方法。这些编码方法的区别在于处理高对比度或高度复杂的物体表面的鲁棒性,以及二值边界定位的可靠性。下图示意了两种编码方法(简单编码和格雷编码)。如图所示,码字的变化与相位图的2𝜋不连续位置一致。如果二值码序列是由二值图像序列唯一确定的,则可以唯一地确定条纹的阶数,从而逐像素地展开相位。
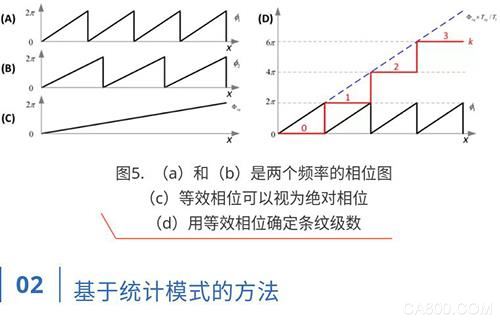
通过参考不同频率条纹图的相位,可以确定每个像素的绝对条纹级数k(x,y),这种方法通常被称为多频率相移方法。多频相移法最初是为激光干涉测量而发展起来的,同样适用于DFP系统。
对于不同周期的条纹图有如下性质:

等效相位可用下面公式计算:
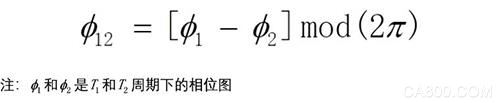
通过不同频率的多幅相位图,使得等效条纹周期可以覆盖整个条纹投影范围,这样等效相位在投影范围内就不需要任何相位展开属于绝对相位,即:
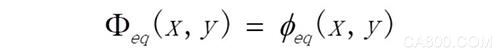
该等效展开相位还可以通过以下“反向相位展开公式”确定高频相位的条纹级数k(x,y):
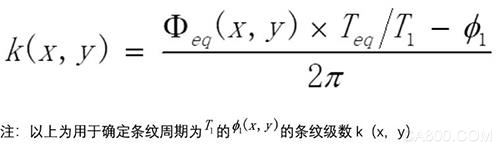
由于噪声的影响,通常使用两个以上频率的相移条纹图。为了提高条纹级数确定的稳健性,通常递归执行反向相位展开步骤:使用最终等效相位确定第二长等效条纹周期相位的条纹阶数,然后利用第二长等效相位来展开具有第三长等效条纹周期的相位,依此类推。
上述时间相位展开方法需要多个附加图像来确定绝对条纹级数。对于高速应用,需要减少投影张数。因此,利用一张随机图片替代几个灰度图片来编码条纹顺序k(x,y)。其基本思想是投影仪投影一个随机图片,并采用立体匹配的方法来寻找投影图像和摄像机拍摄图像之间的粗略视差图。如:ELAS[8]算法可以用来确定视差。一旦粗略视差图被确定,相机像素与投影仪像素粗略的关联也可以被确定。由于随机图片不能提供高精度匹配关系,导致基于该随机图片确定的条纹级数与相位上的2𝜋不连续性不能精确对应。因此,需要利用包裹相位作为约束进行精细调整,进而获得绝对相位。流程如下图所示[9]:

参考文献:
[1] Song, Zhang, Shing-Tung,等. High-resolution, real-time 3D absolute coordinate measurement based on a phase-shifting method.[J]. Optics Express, 2006.
[2] Ghiglia D C, Pritt M D, editors. Two-dimensional phase unwrapping: theory, algorithms, and software. New York: John Wiley and Sons; 1998.
[3] Su X , Chen W . Reliability-guided phase unwrapping algorithm: a review[J]. Optics & Lasers in Engineering, 2004, 42(3):p.245-261.
[4] Zhang S . Flexible 3D shape measurement using projector defocusing: extended measurement range. Opt Lett 2010;35(7):931–3 .
[5] Hall-Holt O , Rusinkiewicz S . Stripe boundary codes for real-time structured-light range scanning of moving objects[C]// Eighth IEEE International Conference on Computer Vision Iccv. IEEE, 2002.
[6] Wang Y , Zhang S , Oliver JH . 3-D shape measurement technique for multiple rapidly
moving objects. Opt Express 2011;19(9):5149–55 .
[7] Huntley J M , Saldner H O . Temporal phase-unwrapping algorithm for automated interferogram analysis[J]. Applied Optics, 1993, 32(17):3047-3052.
[8] Geiger A , Roser M , Urtasun R . Efficient large-scale stereo matching. In: Proceedings of the 2010 Asian Conference on Computer Vision; 2010. p. 25–38 .
[9] An Y , Zhang S . Three-dimensional absolute shape measurement by combining binary statistical pattern matching with phase-shifting methods. Appl Opt 2017;56(19):5418–26 .