红外线测温法的原理是对精确监测系统进行详细说明的重要前提。遗憾的是,许多用户没有花时间来了解基本原理,因此他们会认为非接触式温度测量是不精确的。
温度测量可以分为两类:接触式和非接触式。接触式热电偶、RTD和温度计在温度测量应用中最为普遍。由于测量的是它们自身的温度因此它们必须接触目标,它们的响应相对较慢,但它们比较便宜。非接触式温度传感器测量目标发射的红外线能量,它们响应快,通常用来测量移动目标或间歇性目标,真空中的目标,以及测量由于恶劣环境、结构限制或安全隐患而无法接近的目标。它们的成本较高,但在某些情况下,它们的成本与非接触式设备相当。
红外线辐射由艾萨克·牛顿爵士于1666年发现,他通过让白色光透过玻璃棱镜,将白色光束分解成彩虹的颜色,从阳光中分离出电磁能量。1800年,威廉·赫歇尔爵士进一步测量了每种颜色的相对能量。他还发现了可见光以外的能量。20世纪初,普朗克、斯蒂芬、玻尔兹曼、维恩和基尔霍夫进一步确定了电磁波谱的活动,并且发展了用来确定红外线能量的定量数据和方程式。
这项研究使人们有可能利用基本黑体辐射曲线(参见图1)确定红外线能量。从该图中可以得出,温度高于-273?C的物体辐射出的能量数量与其温度的四次方成比例。黑体辐射概念是红外线测量法的基础。然而,术语"发射率"为这些基本物理定律增加了变数。发射率衡量灰体(非黑体)放射出的热辐射量与相同温度的黑体的热辐射量之比。(灰体指在所有波长具有相同光谱发射率的物体;非灰体指发射率随波长而改变的物体,例如铝。)
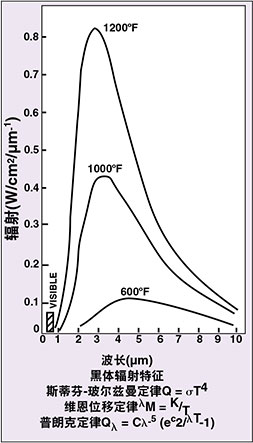
图1:如在600?F ~ 1200?F温度范围内黑体发射的能量分布的曲线所示,主辐射位于0.5-14 μm的红外区,远离可见光区。
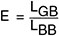
能量守恒定律说明辐射(吸收)的透射、反射和发射的系数之和必须等于1:
tλl + rλ + aλ = 1
并且发射率等于吸收
Eλ = aλ
因此:
Eλ = 1 - tλ - rλ
此发射率系数可以作为变量放入普朗克方程式中,描述相对于波长的物体表面特征。大多数被测物体是不透明的,发射率系数可以简化成:
Eλ = 1 - rλl
玻璃、塑料和硅等材料是例外,但是通过选择适当的光谱滤光,可以在这些物体的不透明红外线区测量它们。
通常,对于发射率误差会有很多混淆之处,但用户只需记住下面四条:
-
- 红外线传感器不能辨别颜色,这是固有的。
-
- 如果目标反光(例如镜子),请注意,您不仅仅按照需要的那样测量发射的辐射能量,而且还要测量反射的辐射能量。
-
- 如果可以看透目标,需要选择红外线滤光(例如,在5μm波长时玻璃是不透明的)。
-
- 10项应用中有9项不需要绝对温度测量。重复性和无漂移操作提供了严密的温度控制。
如果表面闪光,可手动或者自动进行发射率调整来校正发射率误差。对于大多数应用,这是一种简单的办法。在发射率变化并且造成处理问题时,请考虑使用双波长或多波长辐射测量法解决发射率问题。
设计元素
红外线温度计有种类繁多的配置,包括光学器件、电子器件、技术、尺寸和保护性壳体。但它们都具有一系列红外线能量接收组件和电子信号输出组件。基本组件系列包括汇聚光学器件、镜头和/或光纤、光谱滤光以及探测器作为前端。动态处理有多种形式,但是可以总结为放大、热稳定性、线性化以及信号调节。普通窗户玻璃在短波长范围内适
用,石英适用于中波范围,锗或硫化锌适用于8~14 μm波长范围。光纤可用于0.5~5.0 μm波长区。
从应用的观点看,光学器件的主要特征是视场(FOV),即在指定距离处目标尺寸是多少? 例如,在一种普遍采用的透镜系统中,15英寸工作距离处目标直径为1英寸。根据平方反比定律,通过将距离加倍(30英寸),目标区域理论上也加倍(直径为2英寸)。目标尺寸(测量区域)的实际定义将因供应商而异,并且取决于价格。其它光学配置从适用于近距离精密测量的小光斑器件(直径0.030英寸)到适合远距离瞄准的远距离光学器件(距离30英尺时直径为3英寸),不一而足。注意,如果目标占满视场(FOV),工作距离就不应影响精度,这一点很重要。在一种视场(FOV)测量技术中,可变因素是信号损失和直径。一条严格的规则是能量减少量为1%,但可以在一半功率或63.2%功率时提供一些数据。
对准(瞄准)是另一个光学方面的因素。许多传感器没有这种功能;透镜对准表面,测量表面温度。这种结构可用于不需要高精度的大目标,例如卷筒纸。对于使用小光斑光学器件的小目标,以及对于在远距离监测中使用的远距离光学器件,提供有目视瞄准、瞄准灯和激光瞄准。
选择性光谱滤光通常将短波滤光片用于 高温应用(大于1000?F),将长波滤光 片用于低温测量(–50?F)。很明显,这 与黑体能量分布曲线拟合,并且还有一 些技术方面的优势。例如,高温/短波使 用热稳定性极强的硅探测器,而且短波 设计最大限度减小了发射率变动造成的 温度误差。其它选择性滤光用于塑料薄 膜(3.43 μm和7.9 μm)、玻璃(5.1 μm)和火焰不敏感区(3.8 μm)。
多种多样的探测器的选择是为了来最大限度利用传感器的灵敏度。如图2中所示,PbS灵敏度最高,热电堆灵敏度最低。大部分探测器是光伏型(在通电时输出电压)或光导型(在激励时改变 电阻)。这些探测器响应迅速、灵敏度高的代价就是热漂移,可以通过多种方法解决热漂移,包括温度补偿(热敏电 阻)电路、温度调节、自动校零电路、斩波(AC和DC输出)以及等温保护。可提供不同程度的无漂移操作,无漂移操作取决于设备价格。
在红外线温度计的电子设备组件内,探测器的大约100-1000 μV的非线性输出信号得到处理。信号被放大1000倍,并经过调节和线性化处理,最终输出的是线性mV或mA信号。趋向于提供4 ~ 20 mA输出,以便将环境电噪声干扰降到最小。
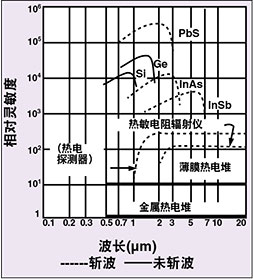
图2:若要优化红外线感应系统的响应,必须考虑探测器的光谱响应和调制特征
这种信号可以转变成RS 232信号,或者提供给PID控制器、远程显示屏或记录器。其它信号调节选项包括通/断报警、适用于间歇目标的可调峰值保持功能、可调响应时间和/或采样保持电路。
红外线温度计的平均响应时间大约为300ms,但是可以使用硅探测器获得大约10ms的信号输出。现实中,很多仪器都拥有可调节响应功能,可对接收的噪声信号进行衰减,并且可对灵敏度进行现场调节。并非总是必须提供最快的响应。 但是有一些涉及感应加热以及其它类型的应用,它们要求大约10-50 ms的响应时间,可通过红外线测温法获得。
单波长测温法
基本单波长设计用于测量表面在规定波长所发射的总能量。配置包括带简单远程仪表的手持式探头、可同时查看目标和温度的复杂便携式设备,以及记忆和/或打印输出功能,不一而足。在线固定安装式传感器从配备远程电子设备(OEM设计)的简单小型探测器到拥有远程PID控制的坚固耐用设备不等。纤维光学器件、激光瞄准、水冷、CRT显示器和扫描系统也包括在用于过程监控和控制应用的选件中。在尺寸、性能、耐用差异。
过程传感器配置、红外线光谱滤光、温度范围、光学器件、响应时间和目标发射率是重要的设计元素,它们影响性能,必须在选型过程中仔细考虑。
传感器配置可以是简单的便携式,或两线制变送器,还可以是复杂的加固型感应装置或扫描设备。目视瞄准、激光瞄准、无瞄准、光纤、水冷、输出信号及远程显示可以笼统地代表各种不同可选功能。这在某种程度上存在主观性,需要进行设计审查。多数情况下,如果是简单应用,例如测量卷筒纸温度,简单的低成本传感器就可以应付了;如果是复杂应用,例如在真空室内测量或者测量小目标,则更先进的传感器将是更好的选择。
红外线光谱响应和温度范围的选择与具体应用有关。短波适合高温测量,长波适合低温测量,这符合黑体能量分布曲线。如果涉及透明目标,例如塑料和玻璃,则需要使用选择性窄带滤光。例如,聚乙烯塑料的CH吸收光谱带为3.43 μm,,在此范围内聚乙烯塑料是不透明的。通过在该范围内滤光,发射率因素得以简化。同样,大多数玻璃类材料在4.6 μm光谱带时变得不透明,在5.1 μm范围内进行窄带滤光就可以精确地测量玻璃表面温度。另一方面,要透过玻璃窗观察,在1-4 μm区域被滤光的传感器允许您透过玻璃窗测量真空室和压力室温度。在测量这类舱室温度时,另一个选择是使用带有真空衬套或压力衬套的光纤电缆。
光学特征和响应时间是两个传感器特征,在允许15英寸处标准视场约为1英寸以及响应时间小于 <1秒就足够了的多数 应用中,它们都不是问题。然而,如果 应用要求测量小目标或者快速移动的间 歇性目标,可以使用小光斑(直径0.125 英寸)和超小光斑(直径0.030英寸)器 件,但价格昂贵。同样,远距离瞄准( 距离目标10~1000英尺)时也需要进行 光学调整,因为标准视场(FOV)将变得过 大。在一些情况下,双波长辐射测量法 可用于这类应用,例如,接线和远距离 瞄准。采用光纤前端,可以不必再在恶 劣环境中使用电子元件、消除了电噪声 并且解决了目标接近问题,因而增加了 设计灵活性。它是一种吸引人的设计工 具,有助于解决一些特别的应用问题。
大多数传感器具有可调响应时间,范围为0.2 ~ 5.0秒,一般设置在此范围的中段。快速响应会受到应用中噪声的干扰,而慢速响应则影响灵敏度。感应加热需要快速响应,传送带或卷筒纸监测需要慢速响应以减少应用中的干扰。快速响应型传感器需要使用快速响应型控制器、可控硅电源组件及其它调节器。可以通过下面的方程式确定综合系统
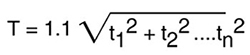
其中:
T = 总响应时间
t1,t2 = 回路中的各个部分
考虑到时间要素,有以下两种过程动态:稳态变化,其中涉及由于过程是动态的而需要严格温度控制的快速运动产品,例如,电线的感应加热。阶跃变化或斜坡响应,与对分批式生产过程中的产品进行极快速加热有关,例如硅片的加温退火。在这些动态应用中,系统响应性和传感器视场(FOV)是关键参数。
很多情况下,被测目标的发射率并不是重要因素。正确选择窄带光谱滤光后,大多数材料的发射率都恒定在0.90±0.05范围内。如果将发射率设定在0.9μm,传感器将倾向于在绝对温度的±5?或10?范围内读取温度。这种应用误差指大约1%或2%的精度变动,然而在现实的红外线测温法中,重复性对于控制至关重要。例如,如果某个产品加热到410?F,传感器读数是400?F,并且传感器读数在390 ~ 410?F之间时您生产出的是优质产品,请使用400作为设定值进行控制。在大多数应用中,无需NIST校准标准即可生产出优质产品。
如果应用需要精确的绝对温度测量和记录,可以根据相关NIST标准校准和认证仪器。另外,需要彻底确定表面发射率仪器。另外,需要彻底确定表面发射率闪亮的滚筒的温度,首先建议测量在闪亮的滚筒上通过的产品。其次,可以使用静态测试条件在传感器上进行发射率调整,以便确定适当设置。再次,双波长测温法也是一种切实可靠的选择。
单波长红外线测温法指在数千种应用中使用的种类繁多却又简单的一种选择技术,在这些应用中,产品温度控制对生产出一贯高质量产品至关重要。
双波长测温法
对于绝对精度是关键所在的更复杂应用,并且在这些应用中产品正经历物理或化学变化,应该考虑使用双波长或多波长测温法。自从20世纪50年代初,比值辐射计的概念就已经存在,但是最近的设计和硬件改进提高了性能、提供了低温功能并且降低了成本。
双波长(比值)测温法涉及测量两种不同波长(光谱带)区域发射的光谱能量。如果在两种波长区域发射率值相同,则可以直接从仪器中读取目标温度。当视场(FOV)的一部分被相对低温的物体遮蔽时(例如瞄准通道上有灰尘、金属网和灰色透明窗口),这类仪器也可以指示目标的正确温度。
这种设计的理论非常浅显易懂,可以用下面的方程式来说明。在这些方程式中,我们使用普朗克方程式计算一个波长区域的能量,然后求出其与另一波长区域能量的比值。
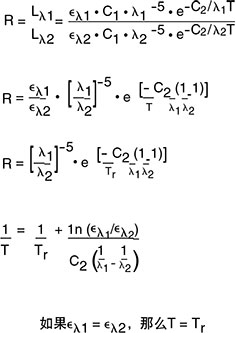
其中:
R = 光谱辐射比
Tr = 表面的比值温度
eλ = 光谱发射率
在此过程中,如果两种波长处的发射率相等(灰体条件),发射率因子消去了方程式,我们发现比值与温度成正比。
通过利用一小段黑体能量分布曲线并且测量不同发射率下的比值,也可以从图形中得到同一概念(参见图3) 使用0.7 μm和0.8 μm光谱段作为窄带滤光片,在最低到0.1的发射率范围内,比值因子恒定在1.428。
同样,任何其它本质上的灰度变化将不影响双波长温度计计算的温度。这些变化包括目标尺寸的变化,例如其直径在测量过程中发生变化的电线或熔化的玻璃流。即便目标比温度计的视场小,这些变化也不影响温度计测量的温度。例如,假定黑体目标仅占据温度计视场的一半,辐射度减少了50%,这种分析不变。另一个示例是目标为烟雾或灰尘所遮蔽或者隔窗(真空室的隔窗)变得模糊不清的情况。只要被遮蔽介质在其辐射衰减过程中没有光谱选择性,至少在温度计使用的波长区域,分析一直是相同的。双波长辐射计测得的温度始终不受影响。
然而,始终有一些我们必须要认识到的限制。双波长对于铝等非灰体不起作用;它很难透过非灰玻璃窗或已加热的耐热玻璃;并且通常在背景比目标更热时,它往往测量背景温度。
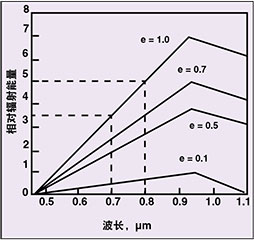
图3:双波长系统通过计算目标在两个相邻波段(例如0.7 μm和0.8 μm)内发射的辐射能量之比值自动消除测量误差
作为一种简单、独特的传感器,双波长 温度计在行业与研究中应用广泛,它可以减少与灰体表面有关的应用误差。图4列举了多种产品的总发射率的示例,这些产品具有与温度有关的变化发射率。例如,大多数用户认为石墨的发射率很高而且恒定不变。然而,实际情况是在环境温度到2000?F范围之内,石墨的发射率在0.4 ~ 0.65之间变化。要获得精确的产品温度测量和控制,在高温下处理这些种类的灰体材料时,应该使用双波长温度计。
还有可用于非灰体材料的多波长温度计,这些材料的发射率因波长而异。在这些应用中,要对与发射率、波长、温度有表面化学有关产品的表面特点进行深入详细的分析。利用这些数据,可以生成使不同波长的光谱辐射与温度相关的算法。
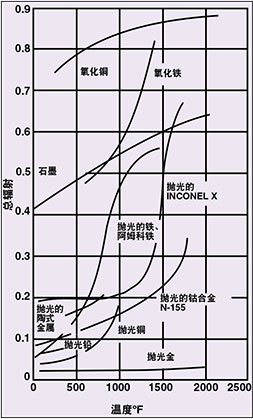
图4:许多材料都有着随温度而变化的发射率级别。我们在此处比较了一些最常用的材料
总结
图5中概述了基本应用元素。待测量目标的表面是主要着眼点。在选择仪器时,用户必须考虑目标尺寸、温度限值、发射率、过程动态(因为它们与视场有关)、光谱响应以及响应时间。为了选择最适合该应用的仪器,对周围环境(例如火焰、红外线加热器、感应线圈和气氛(灰尘、脏污的窗户、火焰、过热)的特征进行描述也很重要。
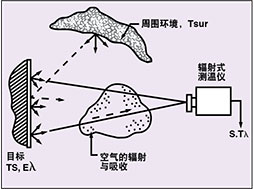
图5:选择非接触式温度测量仪器时,必须要考虑不仅仅是目标及其发射率,还要考虑周围环境以及中间间隔的空气
就性能规范而论,校准精度通常0.5~0.1%的范围内,而大多数传感器的重复性将在0.25 ~ 0.75%的范围内。如果传感器安装 和使用正确,通常会在大约一两个月获得回报。
经HELMERS
PUBLISHING, INC.许可,
转载自《传感器杂志》
(1992年12月)
174 Concord St.
Peterborough, NH 03458
