振动式物位开关在过去几十年得到长足发展,在振动式音叉液位开关的设计中,其音叉振动幅度一般很小,但振动频率较高,一般在1200Hz左右。音叉液位开关采用压电器件实现叉体的振动驱动与检测。当叉体与被测液体接触时,因阻尼使叉体的谐振频率明显降低,振动频率的变化直接反应在压电检测器件的输出信号上,检测电路对频率的变化进行判别并输出一个开关信号。
因此,在音叉液位开关设计过程中,分析当其接触被测液体时,其振动特性和变化规律,就显得尤为重要,而影响或改变音叉振动特性的因素就是介质产生的阻尼。那么,振动式音叉液位开关的阻尼是怎样的呢?
阻尼的相关概念
在对振动式音叉液位开关的阻尼进行分析之前,我们先来看看阻尼的概念。
阻尼,是阻尼是一种能量耗散机制,是指任何振动系统在振动中,由于外界作用或系统本身固有的原因引起的振动幅度逐渐下降的特性,以及此一特性的量化表征。根据不同类型阻尼的物理机制及具体的阻尼现象,或者为了数学计算的方便,物理学家和工程专家在实验的基础上,相继建立了许多描述阻尼力的数学模型。在单自由度有阻尼体系运动方程的基础上,用来描述阻尼常见的三种数学模型分别是粘性阻尼、迟滞阻尼和结构阻尼。
粘性阻尼假定阻尼力与速度成正比,其阻尼力表示为F=-CV。方便地表达阻尼对频率、共振等的影响,是应用最为广泛的阻尼模型,通过将阻尼系数与结构体系的质量、刚度相联系,可以方便地构造出具体的阻尼系数,是目前最常用的阻尼表达方法。粘性阻尼很好地描述了在粘性流体中运动所受到的阻尼作用。
迟滞阻尼又称频率相关阻尼,它与粘性阻尼系数C相对应的阻尼因子是h/θ,其阻尼力表示为F= (h/θ)×V,其中h为材料迟滞阻尼常数;θ为振动频率。砂子的阻尼特性可很好地用迟滞阻尼模型来描述。
结构阻尼理论认为,在固体材料中,阻尼力独立于应变速度,而与应变幅值有关。结构阻尼能很好地描述固体材料的阻尼特性。
振动式音叉液位开关的阻尼分析
振动式物位开关中的音叉液位开关在流体介质中做单自由度的简谐振动,其所受到的阻尼模型视为粘性阻尼模型。由牛顿第二定律,即F=ma,得到其阻尼体系运动方程为
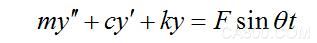
其中介质对音叉振动的阻尼力即为
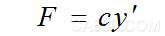
C称为阻尼系数,单位为N.s/m,c与物体的形状、尺寸及介质的性质(如密度、温度、压力、粘度等)有关; y‘为振动速度V。事实上,介质对振动的阻尼力的影响因素并不是单一的,可以肯定的是,阻尼力的大小和振动的速度、介质密度、接触面积都相关,此外,还与振动频率及振幅有关联。在流体介质中,阻尼力大小还与粘度系数有关。在接触面积逐渐增大时,振动速度和振幅都会衰减,阻尼系数c也会随之减小,它是一个不断变化的量。
以上就是有关“振动式音叉液位开关的阻尼分析 ”的介绍,如欲了解更多物位开关、磁翻板液位计等方面的知识,欢迎关注微信公众号:Jiweimeter。(文章摘自:www.levelmeter.cn/yfshow-23-276-1.html,转载请注明出处。)
