基于LMI的无人直升机姿态解耦鲁棒控制器设计

摘  要:无人直升机是典型的多输入多输出系统,具有静不稳、强耦合、不确定的特点。本文首先基于小扰动理论建立起无人直升机的线性模型;然后运用状态反馈进行极点配置,实现了对被控对象四通道间的动态解耦;最后设计了基于LMI的无人直升机H∞鲁棒姿态控制器,解决了模型参数摄动的问题并进行了仿真验证。结果表明所设计的姿态控制器性能良好、结构相对简单,达到ADS-33E-PRF标准LEVEL1的要求。
关键词:无人直升机;极点配置;解耦;线性矩阵不等式(LMI);H∞鲁棒控制

中图分类号:TP302.1    文献标识码:A    文章编号:1003-7241(2013)07-0009-05

1  引言 
目前,随着国民经济的迅速发展,微型无人直升机在越来越多的领域得到应用,例如在消防、电力线缆巡检、反恐、救灾等场合都已经出现了微型无人直升机的身影[1]。但是微型无人直升机具有不稳定、强耦合、不确定、易进入涡环状态、操纵功效和抗风能力差的特点,这就导致无人直升机控制难度大,并对飞行控制系统的各种性能均提出严峻考验。另外,随着进一步的战事和民用的需求,未来的无人直升机将在极为恶劣的环境下完成复杂的战术和战略使命,并且还需要能够实现精确的自动着陆以及故障状态下的容错、自修复控制等,这些都对无人直升机的飞行控制系统提出了极为苛刻的要求。采用传统基于PID的单回路控制器设计方法显然已无法满足高性能无人直升机控制系统的设计要求,因此,进一步加强对无人直升机的先进飞行控制理论和方法的研究,对促进我国无人直升机先进飞行控制技术发展具有重要理论和现实意义。
本论文旨在对面向无人直升机的先进自主飞行控制算法进行研究,为自动飞行控制器的后续设计工作提供指导。基于上述现实原因,本论文的研究内容不仅具有显著的理论和现实意义而且是一个前沿的研究领域[2]。


2  无人直升机动力学模型 
2.1  操纵力学结构

2.2  动力学模型

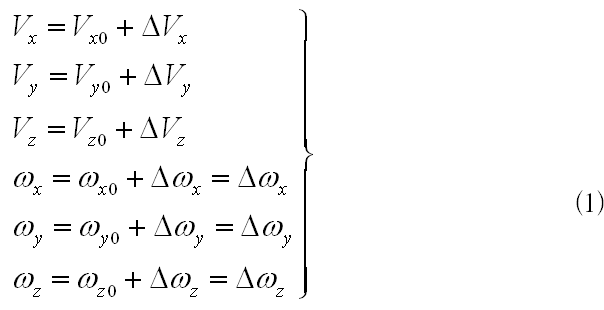
将(1)(2)所描述的参数关系分别带入到直升机受力分析模型[3]之中,并忽略所有的二阶小量,即进行线性化后可以得到下列结果:

综合式(3)(4)可以得到直升机定常直线飞行时的9阶小扰动线化运动方程的标称状态空间表达式:

3  基于状态反馈的极点配置解耦
3.1  状态反馈解耦控制算法

3.2  期望回路形状
根据ADS—33E—PRF标准,以LEVEL1为设计目标,可以选择四个通道上期望回路形状为[5]:

4  基于LMI的H∞鲁棒控制器设计 
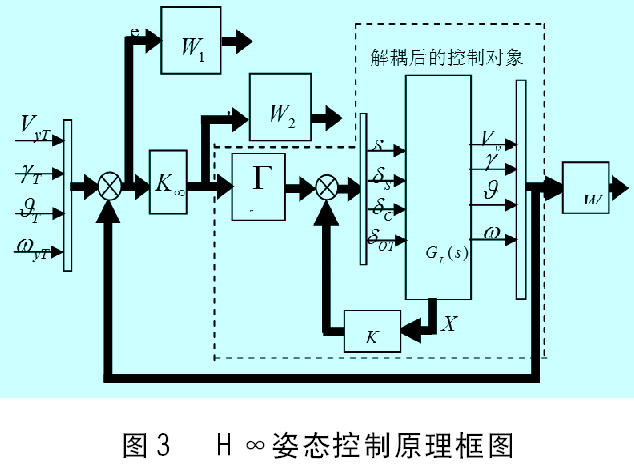
无人直升机具有强烈的静不稳、强耦合、不确定性特点。采用极点配置方法解决了4通道之间的耦合问题。但是,无人直升机受扰之后模型参数摄动非常明显,该问题可以采用H∞鲁棒控制器给予解决。无人直升机姿态控制器实质上是一个具有良好跟踪性能的四输入——四输出控制器[6,7,8]。原理示意框图如图3所示:
其中,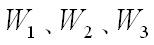为权重函数;为H∞控制器。

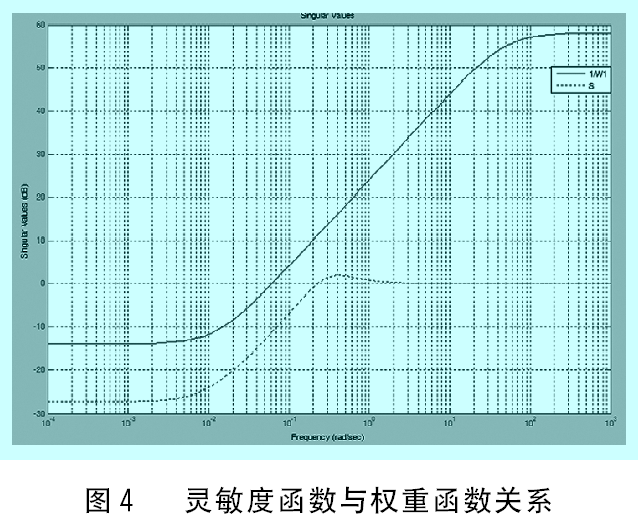
4.1  权重函数选取

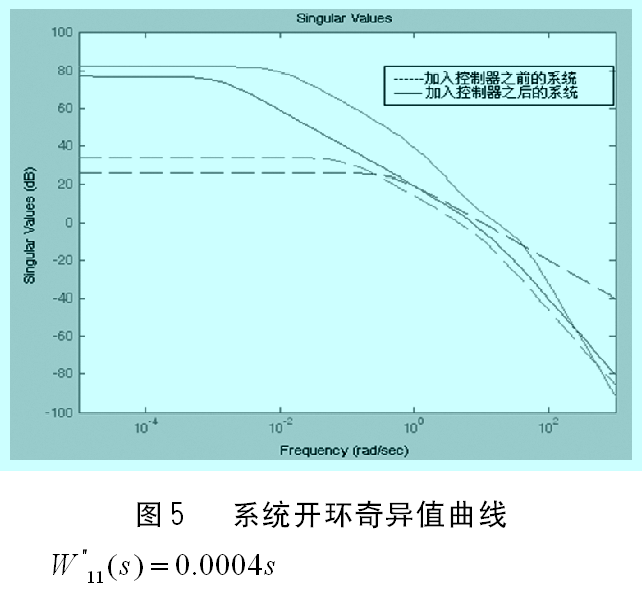
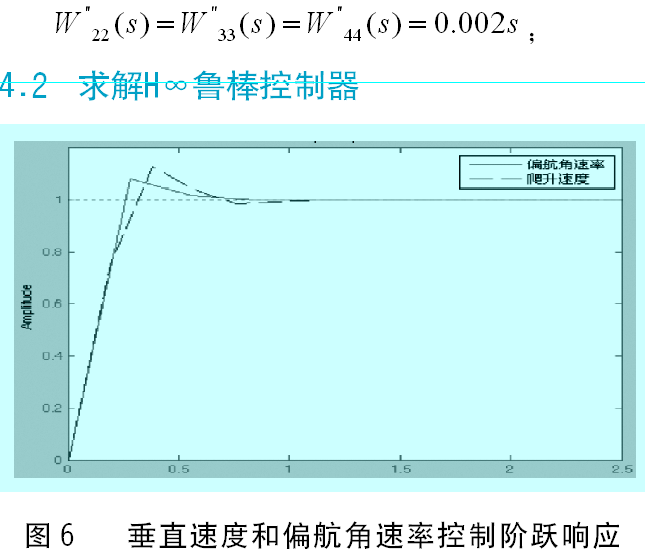
5  仿真实验结果及性能评估

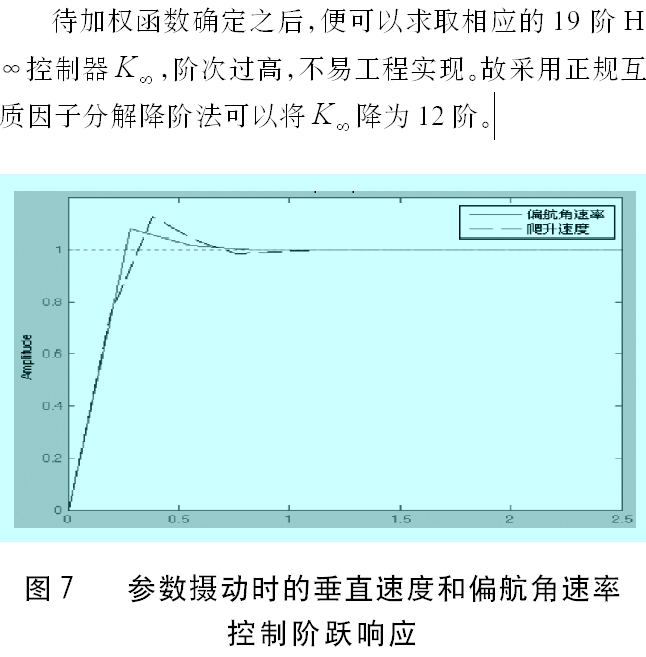
图7表明动态性能和解耦效果很好,当总距通道和偏航通道存在操纵输入时,本通道的调节时间很短(0.8s左右)、超调很小(11%左右)并且几乎不存在通道耦合。图7表明在被控对象参数摄动时,设计的鲁棒控制器仍然可以完成控制任务,效果与摄动之前没有明显恶化,并且存在摄动的通道对其它通道的影响不大。


6  结束语
本文首先比较详细地介绍了小型无人直升机完备的空气动力学模型建立过程;然后运用状态反馈进行极点配置,把无人直升机解耦成四个相互独立的通道;最后运用回路成形理论设计了H∞鲁棒控制器,解决了无人直升机模型参数摄动范围大的问题。论文还对所设计的控制器进行了仿真验证,结果表明控制效果达到了ADS—33E—PRF标准LEVEL1的要求。本文为设计基于先进算法的无人直升机自动驾驶仪进行了理论方面的探讨,为控制器后续工程实现、半实物仿真和试飞验证奠定基础。

参考文献:
[1] LUI SHA,Using Simplicity to Control Complexity[J].IEEE SOFTWARE July/August,2001:20-28.
[2] ISIDORI A,MARCONI L,SERRANI A.Robust nonlinear motion control of a helicopter[J].IEEE Transactions on Automatic Control,2003,48(3):413—426.
[3] 高正,陈仁良.直升机飞行动力学[M].北京:科学出版社,2003.
[4] 郑大钟.线性系统理论[M].北京:清华大学出版社,1998.
[5] SHI XIAO-PING, DUAN Hong-JUN.Nonlinear H∞ Attitude Control of Flapping Wing Micro Aerial Vehicle[J].ournal of System Simulation,2007,(10):4499-4503.
[6] VAN DER SCHAFT.L2 Gain Analysis of Nonlinear System and Nonlinear State Feedback H∞ control[J].