引言：振华港机移船绞车项目选用丹佛斯690V、355kW的变频器，要求变频器具有100%转矩连续制动的能力。而丹佛斯变频器设计指南上只保证了此型号变频器100%制动转矩，40%制动率的能力。但根据对此型号变频器硬件和技术数据的仔细分析，我们发现此变频器实际具有比标称值大得多的制动能力。下面就是估算丹佛斯变频器实际制动能力和优化选择制动电阻的详细办法。
计算中需要用到的丹佛斯FC302P355KT7E5MH2B变频器的基本数据：
直流中间环节制动动作电压：1084 VDC
散热片最高温度：85 ℃
制动晶体管：DP400C1700S100734，两块并联。
单块制动晶体管标称电流400A；
影响丹佛斯变频器制动能力的主要因素
影响变频器制动能力的主要因素为制动晶体管的导通电流能力、变频器整机的散热能力和制动晶体管的散热能力。下面逐一分析。
首先，分析制动晶体管的导通电流能力:
按直流制动电流最大值Ibrake_max = 400 × 2 = 800 A
制动晶体管瞬时最大制动功率Pbrake_peak = 800 × 1084 = 867 kW
此值高达变频器标称功率的244%，因此可知制动晶体管的导通电流能力不是制约变频器制动能力的关键因素。
其次分析变频器工作于连续制动状态时，变频器的整机散热能力。
设变频器在全速、满载时发热量为100%，则变频器的整机散热能力也为100%。
按丹佛斯技术资料，可知此时：
变频器整流部分发热量是26%，变频器逆变部分发热量是74%。
再假设连续制动时，制动晶体管是连续工作的，制动晶体管上的电流为IBR
根据能量守恒定律，P制动晶体管 = P电机
推导，IBR ×VDC =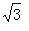
×Io ×Vo ×0.86(功率因数) ×0.93(电机效率)
对于T7机型，VDC = 1084 V，电机额定电压Vo = 660V，
则 IBR = 0.843 Io = 0.937 Io_av
因此有统一的结论： IBR ≈ Io_av，即制动晶体管上的电流与电机电流平均值相同。
因为输出有3路，制动只有1路，所以可以一般地认为：
制动晶体管的发热量 = ×逆变部分发热量
则连续制动时的变频器整机发热量 =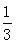
逆变部分发热量 + 制动部分发热量
= 74% + 74% / 3 = 98.7%
≤ 100%
所以得出结论：变频器连续制动时的发热功率不大于变频器连续电动时的发热功率，因此变频器的整机散热能力不是制约变频器制动能力的关键因素。
进一步的分析表明制约变频器制动能力的关键因素是制动晶体管的散热能力，下面的估算将围绕制动晶体管的散热能力展开。
制动晶体管的发热功率和结温限制
制动晶体管的发热功率 = 导通损耗 + 开关损耗
一、 制动晶体管的开关损耗
1. 假设负载是纯电阻，开关时的电压、电流是线性变化的。
单次开（关）的损耗 =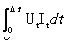 
= 
= 
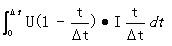
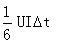
其中Δt为开关时间，
制动晶体管的总开关损耗PSW = 单次开（关）损耗× fSW × 2
= 
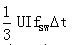
不过这一假设太理想化了。
2. 假设负载含电感，开通、关断的电压、电流波形如下：
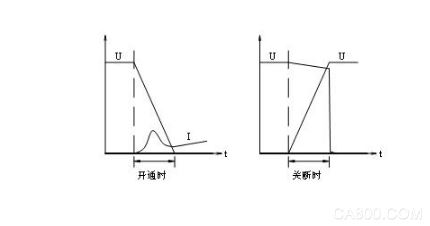
开通损耗，与模块中的快恢复二极管的特性相关，难以计算。估算中以固定值0.01 J代入。
关断损耗 =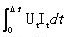 
≈
= 
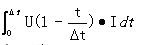
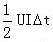
制动晶体管的总开关损耗 PSW = ( 0.01 +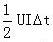
)× fSW
本着安全的原则，计算中选择较大的 PSW = ( 0.01 +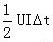
)× fSW
fSW ，参阅丹佛斯变频器技术资料，制动晶体管的开关频率fSW = 1.2 kHz
Δt，参阅《FC300设计指南》中的du/dt数据：2261 V/μS
推测Δt = 1084 / 2261 = 0.48 μS。计算时取Δt = 0.5 μS
二、 制动晶体管的导通损耗
1． 制动晶体管的导通压降-导通电流（VCE-IC）曲线
附件一中没有此曲线，但根据附录1中制动晶体管DP400C1700S100734的特征参数：
VCES=1700V
IC=400 A（TC=80℃）
VCE(sat) = 2.0V（IC=400A，TJ=25℃）
VCE(sat) = 2.4V（IC=400A,TJ=25℃）
查到三菱CM400DY-34A和英飞凌FZ400R17KE3的晶体管特性与其完全相同，因此可以使用他们的“VCE-IC”特性曲线，获得制动晶体管的导通压降。
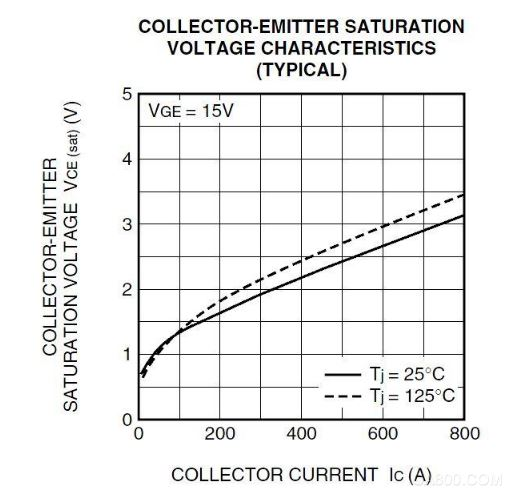
此晶体管是正温度系数的IGBT，所以我们只需要取发热最厉害的125℃结温时的数据，将其数字化，得表一：
电流IC（A） 50 100 150 200 250 300 350 400
VCE(sat) （V） 1 1.35 1.6 1.8 2 2.17 2.3 2.4
2． 制动晶体管的导通损耗
PCND = VCE(sat) × IC
三、 制动晶体的结温升：
制动晶体管的结温升TRISE = ( Rth(j-c) + Rth(c-f) ) × PLOSS
其中PLOSS 为制动晶体管开关损耗和导通损耗之和，PLOSS = PSW + PCND
其中Rth(j-c) 为制动晶体管硅片到模块散热片的热阻，从附件一查到Rth(j-c) = 0.06 K/W
其中Rth(c-f) 为制动晶体管模块散热片到变频器散热片的热阻，附件一没有此数据，但是英飞凌模块DF400R12KE3的封装与丹佛斯制动晶体管的封装完全相同，内部机构相似，而且注意到他们的晶体管热阻Rth(j-c)也相同，所以计算中可以参照英飞凌模块DF400R12KE3的数据，取 Rth(c-f) = 0.03 K/W
有了以上数据，再依据制动晶体管的最高工作结温不能超过125℃的限制条件，就能计算丹佛斯变频器的最大连续制动能力了。
制动晶体管的制动功率-制动率曲线
首先关于温度裕度的说明，为了变频器的安全运行，必须保留一定的IGBT工作结温裕度，但是由于丹佛斯变频器散热片的温度检测取自逆变模块内部，而散热片的实际温度要比逆变模块内部低，此温差已经使我们的计算有相当大的温度裕度。
最大允许结温升TRISE-MAX = 最高工作结温 – 散热片最高温度 = 125-85 = 40 ℃
计算步骤：
1．首先假设一个制动功率，比如355kW，然后按此功率算出制动晶体管的结温升TRISE；
2．如果TRISE ≤ TRISE-MAX ，说明在此制动功率下能够连续制动，
如果TRISE > TRISE-MAX ，则说明在此制动功率下不能连续制动，制动率Duty% =
表二、制动晶体管结温计算表：
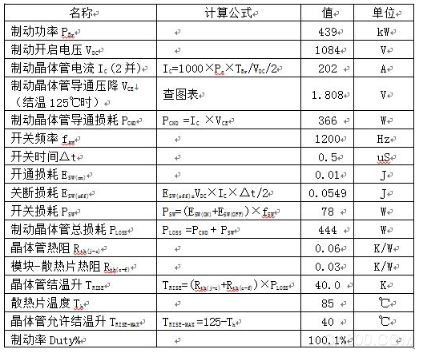
按上述步骤选择多个制动功率，得到表三，制动功率-制动率数据表格:
制动功率(kW) 532 497 461 439
制动率(%) 76.9% 84.5% 93.6% 100.0%
绘制成，曲线一、制动功率-制动率曲线：
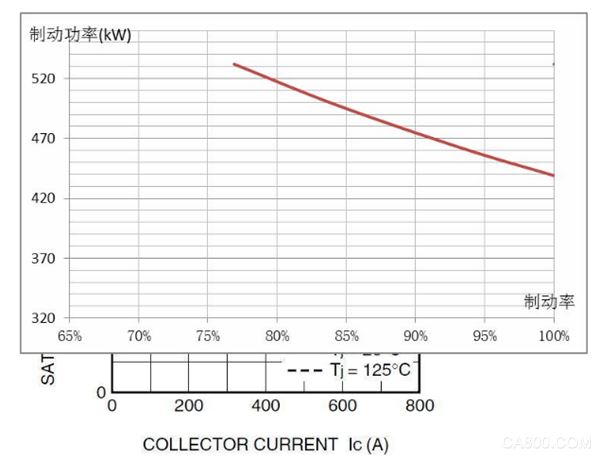
从制动功率-制动率曲线可以发现丹佛斯FC302P355KT7E5MH2B变频器具有超过100%制动转矩连续制动的能力。
制动功率-制动电阻关系曲线
解决了制动功率-制动率的问题，接下来还有更实际的问题需要解决—制动电阻的取值。有些变频器厂家提供了不同制动率下的制动功率-制动电阻关系曲线，供用户作选取制动电阻之参考，但是丹佛斯变频器设计指南中暂无此数据，所以我们用手工计算的办法绘制了一张100%制动率时的制动功率-制动电阻关系曲线，供用户参考。
计算步骤说明如下：
1．首先选取一电阻值，比如3Ω，然后根据此制动电阻值可以知道制动电流和制动功率，利用表二可以算出连续制动时制动晶体管的结温升TRISE。
2．如果TRISE ≤ TRISE-MAX ，说明此阻值下的制动功率PR能够满足100%制动率的要求；
如果TRISE > TRISE-MAX ，则说明此阻值下的制动功率PR只能满足Duty% =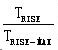
的制动要求，根据PR ×Duty% = PBrake-100% ×100%，可以得到调整后的等效连续制动功率：
PBrake-100% = PR×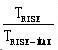
按上述计算办法，选取多个制动电阻值，得到表四，等效连续制动功率-制动电阻数据表：
绘制成，曲线二、制动功率-制动电阻曲线：
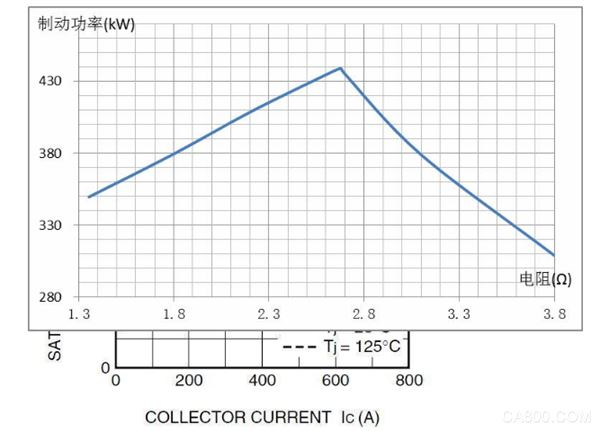
制动电阻的优化选择
首先，制动电阻的最小值受限于制动晶体管的导通电流能力，因此有：
RBrake_min =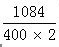
= 1.36Ω
然后，制动电阻的取值决定了变频器的最大瞬时制动功率。在此应用例中，用户要求电机最大制动转矩不小于110%，则PBrake 不小于 355kW×110%×93%(η电机)×98% (η变频器)= 356kW，制动电阻RBrake ≤ 10842/356000 = 3.3 Ω。
小于3.3Ω的制动电阻虽然能够提供更大的瞬时制动转矩，但是将增加制动晶体管的散热负担，因此满足最大制动转矩要求的制动电阻值3.3Ω就是最佳电阻值。
参考文献
[1] FC300 Design Guide. MG.33.BC.02. Danfoss A/S
[2] FZ400R17KE3 Technical Information. REV2.2 2007-3-28. Infineon Technologies
[3] DF400R12KE3 Technical Information. REV3.0 2008-10-23. Infineon Technologies
[4] CM300DY-34A Data Sheet. Feb.2009. MITSUBISHI ELECTRIC
[5] General Consideration for IGBT and Intelligent Power Modules. Sep 1998. MITSUBISHI ELECTRIC
