关键字:
新型Lyapnov函数、模糊控制器、不确定性系统、并行分布补偿原理
导读:
研究了在新型Lyapunov方法下的带有不确定性的T—S模糊模型稳定性及控制器的设计,给出了输入为零时系统稳定的充分条件,并验证了该条件比常用李雅普诺夫函数具有更大的松弛性。基于新型李雅普诺夫函数,对带有不确定性模糊模型设计了线性矩阵不等式形式的模糊控制器,该方法不必知道某一时刻被激活的规则数,同时把一个公共矩阵的寻找分解为p个矩阵的寻找。仿真实验证明,通过应用改进的李雅普诺夫函数设计的模糊控制器,具有良好的鲁棒性,控制效果良好。
1 引言
基于Lyapunov直接判定稳定性[1-3]的方法要求在所有的子系统中找到一个公共的正定矩阵,并要求P满足所有的Lyapunov方程,这是非常困难的。多位学者对此做了进一步的研究[4-6],虽然他们的结果在一定程度上放宽了Tanaka 等人的稳定性判定条件,但也有各自的不足之处。IkedaT等人[4]只考虑了几个模糊子系统之间的相互作用;Zhang JM等人[5]采用的最大隶属度去模糊法与常用的重心法相比较,而没有充分考虑激活度较小的规则对整个系统稳定性的影响。Tanaka等人提出了模糊Lyapunov方法,对隶属函数的导数给出了限定[7],本文应用Rhee等人提出的新型模糊Lyapunov函数,避开了对隶属函数的求导,在一定程度上放宽了稳定条件并给出了更松弛的稳定性条件。







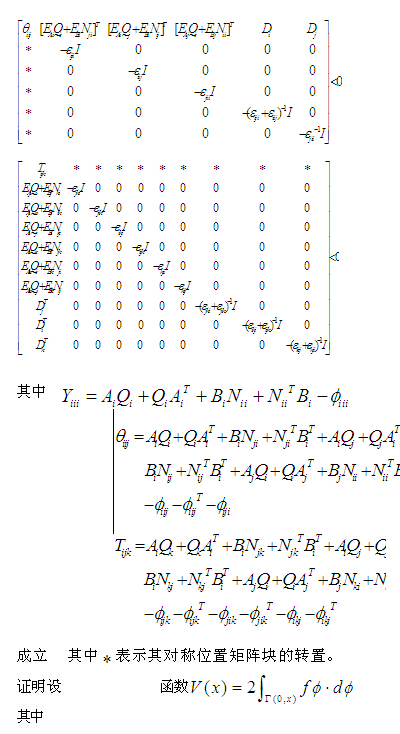

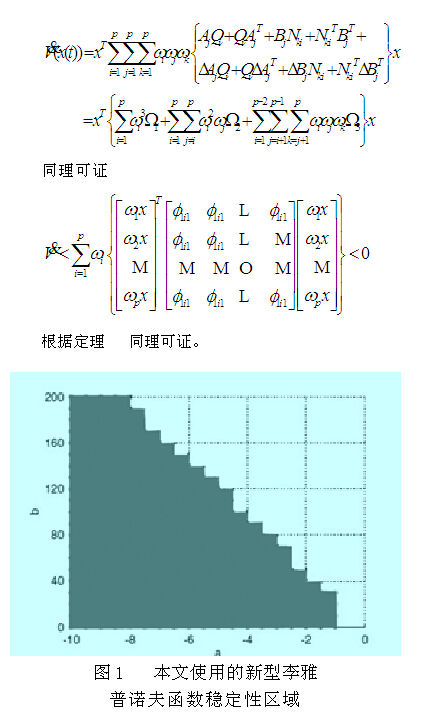
此定理不必知道某一时刻被激活的规则数,把对一个公共矩阵的求解转化为对p个矩阵的寻找,优越于现有的稳定性判定条件,所以定理2有很大的优越性。
3 数值仿真
考虑如下T—S模糊系统
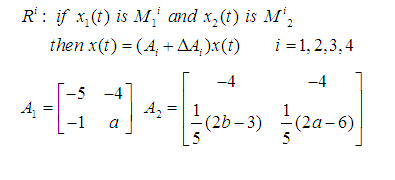
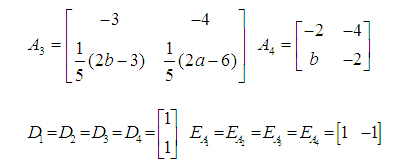
系统的状态矩阵系数a、b的不同取值稳定性范围也不同。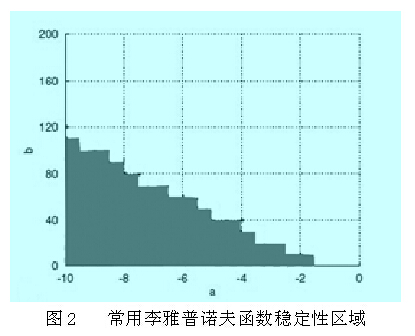
其中阴影部分表示确定的稳定性区域,从图中可以看出定理1对应的稳定性范围比常用Lyapunov函数的稳定性范围更广。
考虑下面不确定T—S模糊系统.


运用matlab对该闭环系统进行仿真,状态初始值为[2 4 -2]的系统仿真曲线如下:
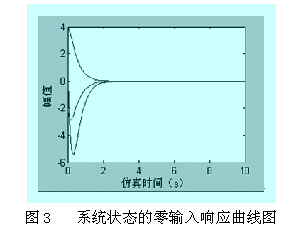
4 结束语
本文应用了文献[8]提出了新型Lyapunov函数对含有不确定性的模糊系统进行了控制器的设计,得到了含有不确定性的连续T—S模糊系统稳定性的充分条件,运用PDC方法设计了模糊控制器,仿真后得到了较为满意的仿真效果。